Wenn Ihnen die vielen Sechsecke bei der Beschreibung der Pflanzengifte nicht viel sagen, so sollten Sie dieses Kapitel lesen, um einen ersten Einblick in die Chemische Zeichensprache zu gewinnen. Das Verstehen dieser Sprache ist durchaus nicht so schwer, wie es vielleicht im Rückblick auf Ihren Chemieunterricht erscheinen mag. Wagen Sie daher den Schritt und erlernen Sie die Chemische Zeichensprache:
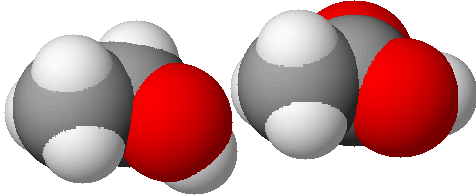
Nehmen wir zwei Chemikalien, die jedem bekannt sein dürften: Ethanol (links), der gewöhnliche Alkohol, und Essigsäure (rechts), wie wir sie aus Essigessenz oder Weinessig kennen. Wollten wir diese einfachen Chemikalien möglichst realistisch darstellen, so müßten wir folgendes Modell wählen:

Hierbei stehen die schwarzen Kugeln für Kohlenstoff, die roten für Sauerstoff und die weißen für Wasserstoff. Es ist leicht einzusehen, daß diese Darstellungsmethode bei größeren Molekülen versagt. Daher geht man zu einfacheren Strichmodellen über (die Buchstaben sind die Elementsymbole, wie sie auch im Periodensystem verwendet werden, also H für Wasserstoff, C für Kohlenstoff und O für Sauerstoff; daneben werden wir noch dem N für Stickstoff, dem P für Phosphor und dem S für Schwefel begegnen):
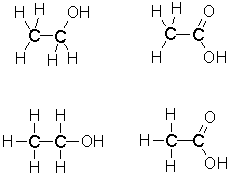
Die obere Reihe (räumliche) der beiden Darstellungen ist dabei etwas näher an der Realität als die untere, die untere Reihe jedoch auch bei größeren Molekülen leichter zu überblicken. Dennoch kommt auch diese Darstellung schnell an ihre Grenzen. Das am häufigsten zu zeichnende Element ist der Kohlenstoff. Es bedeutet schon eine immense Erleichterung, einfach in den Formeln das C wegzulassen:

Jetzt kommt die Chemie ins Spiel: Kohlenstoff ist immer vierbindig, d.h. um einen Kohlenstoff befinden sich immer vier Bindungstriche, wobei auch mehrere Bindungen zu einem Nachbar geschlossen werden können (wie z.B. mit einem der beiden Sauerstoffatome in der Essigsäure; sog. Doppelbindung). Bis zu drei Bindungen (sog. Dreifachbindung) zu einem Nachbar sind möglich, etwa mit Stickstoff (z.B. Cyanwasserstoff) oder mit einem zweiten Kohlenstoff (z.B. Acetylen). Wenn dem so ist, kann man sich das Zeichnen der Wasserstoffatome einfach sparen, denn jeder kann die gezeichneten Bindungen zählen und die erhaltene Zahl von 4 abziehen, um zu bestimmen wieviel Wasserstoffatome am betreffenden Kohlenstoffatom noch sitzen müssen. Bei Hetereoatomen (so bezeichnet man alle Atome im Molekül mit Ausnahme von Kohlenstoff und Wasserstoff) wird der Wassserstoff aber immer angegeben. Außerdem dürfen die Wasserstoffatome nur weggelassen werden, wenn auch kein C hingeschrieben wird:
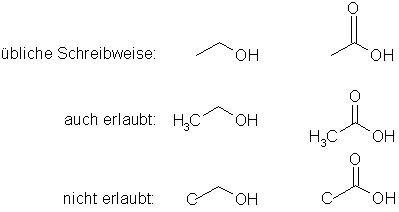
Wenn sich chemische Formeln nur geringfügig unterscheiden, müssen Sie nicht jede Formel einzeln aufzeichnen sondern können den veränderlichen Teil mit einem »R« für Rest kennzeichnen und z.B. in einer Tabelle die verschiedenen Reste den verschiedenen Verbindungen zuordnen. Zur Verdeutlichung sind hier die Formeln auch nochmal einzeln aufgeführt:
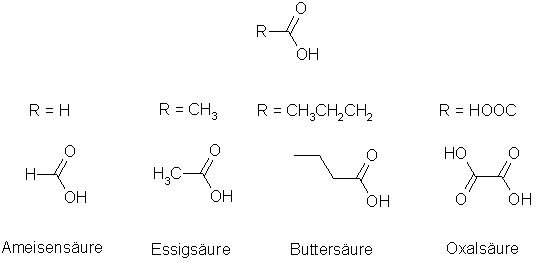
Das »R« können Sie auch dann verwenden, wenn dem Rest für den zu erläuternden Sachverhalt keine Bedeutung zukommt und Sie sich nur auf einen Teil des Moleküls konzentrieren wollen.
Soviel zur Erklärung der Strichformeln. Manchmal sind in Strichformeln Wasserstoffatome eingezeichnet, teils mit punktierten Linien, teils mit Keilen. Dies hat damit zu tun, daß es dann mindestens zwei verschiedene Verbindungen gibt, die in die Ebene gepresst gleich aussehen. Mit einem Keil versehene Bindungen zeigen mit der breiten Seite des Keils zu Ihnen (aus der Ebene heraus), gepunktete Bindungen zeigen von Ihnen weg:
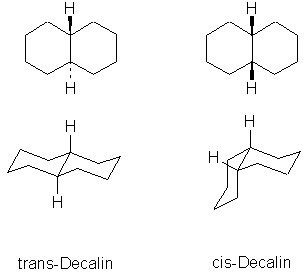
Die unteren Formeln sind die räumliche Darstellung der darüberstehenden. Die relevanten Wasserstoffatome sind nur zur Orientierung in die untere Formel eingezeichnet.
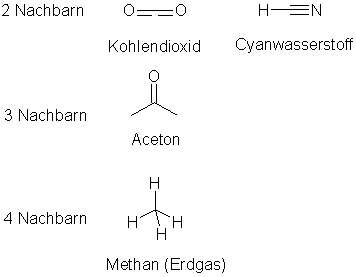
Wie kommt man nun zu der räumlichen Darstellung? Die Regel dazu ist ganz einfach: Die Nachbaratome sind um ein Kohlenstoffatom so anzuordnen, daß sie den möglichst größten Abstand zueinander haben. Hierbei müssen Sie auch an die Wasserstoffatome denken, die Sie der Einfachheit halber nicht eingezeichnet haben. Angenommen ein Kohlenstoffatom hat zwei Nachbaratome (etwa mit je einer Doppelbindung oder ein Nachbaratom mit einer Dreifachbindung und ein Nachbaratom mit einer Einfachbindung), dann ist der größmögliche Abstand gegeben, wenn Zentralatom und Nachbaratome auf einer Linie liegen. Bei drei Nachbaratomen ist der größtmögliche Abstand dann gegeben, wenn alle Atome in einer Ebenen liegen und die Nachbaratome in einem Winkel von 120° angeordnet sind (wie bei einem Mercedes-Stern). Bei vier Nachbaratomen ist der Tetraeder die optimalste Anordnung.
Anhand der folgenden dreidimensionalen Darstellung können Sie sich nochmal ein Bild über die Tetraeder-Struktur von Methan machen:

Fixieren Sie mit jedem Auge ein Modell. Entweder beim unteren oder (wie bei mir) beim oberen Pärchen sollte der 3D-Effekt zu bemerken sein (Aufnahmeverfahren analog zu R. Schubert, c't 18/98, 179). Schauen Sie sich im übrigen nochmal das erste Modell dieser Seite an, ob sie die Tetraederstruktur wiedererkennen. Ein Molekül, in dem alle drei Raumstrukturen zu finden sind, ist Methylcyanacrylat, besser bekannt als Sekundenkleber. Hier ein Kugelmodell davon in einer etwas anderen Form (die blaue Farbe kennzeichnet Stickstoff, die anderen drei Farbcodierungen wurden beibehalten):

Täglich haben wir mit physikalischen Einheiten zu tun, etwa dem Gramm, dem Meter oder auch der Sekunde. Niemand kommt jedoch auf die Idee, die Entfernung zwischen zwei Städten in Zentimetern oder die Größe eines Buches in Metern anzugeben. Es existieren Verkleinerungs- und Vergrößerungsvorsilben, die uns den alltäglichen Gebrauch mit den physikalischen Einheiten erleichtern. Geläufige Vorsilben, etwa Kilo- oder Centi-, sind jedermann bekannt, exotischere, wie Mega oder Giga hat man schon mal beim Computerkauf vernommen, aber was bedeuten sie? Die folgende Tabelle stellt Ihnen die Verkleinerungs- und Vergößerungsvorsilben der physikalischen Einheiten vor:
| Name | Symbol |
Faktor |
Potenz | Bezeichnung | Bemerkungen | ||
| Exa | E | 100000000000000000 | 0 | 1018 | Trillion | ||
| Peta | P |
100000000000000 |
0 | 1015 | Billiarde | ||
| Tera | T |
100000000000 |
0 | 1012 | Billion | ||
| Giga | G |
100000000 |
0 | 109 | Milliarde | In dem Land mit den 50
Bundesstaaten glaubt man, daß es
sich bei einer Milliarde um einen Billion handelt |
|
| Mega | M |
100000 |
0 | 106 | Million | 1 Megagramm (Mg) wir auch als Tonne (t) bezeichnet | |
| Kilo | k |
100 |
0 | 103 | Tausend | ||
| Hekto | h |
10 |
0 | 102 | Hundert | ungebräuchlich; nur in Verbindung mit Liter und Pascal (1 hPa = 1 mbar) | |
| Deka | da |
1 |
0 | 101 | Zehn | ungebräuchlich; nur in Verbindung mit Gramm | |
|
|
1 | 100 | Eins | ||||
| dezi | d |
|
0, |
1 |
10-1 | Zehntel | ungebräuchlich; nur in Verbindung mit Liter |
| centi | c |
|
0, |
01 |
10-2 | Hundertstel | ungebräuchlich; nur in Verbindung mit Liter und Meter |
| milli | m |
|
0, |
001 |
10-3 | Tausendstel | |
| mikro | µ |
|
0, |
000001 |
10-6 | Millionstel | |
| nano | n |
|
0, |
000000001 |
10-9 | Milliardstel | |
| pico | p |
|
0, |
000000000001 |
10-12 | Billionstel | |
| femto | f | 0, |
000000000000001 |
10-15 | Billiardstel | ||
| atto | a |
|
0, |
000000000000000001 |
10-18 | Trillionstel | |
Auch wenn wir uns der Bedeutung der Vorsilben bewußt sind, heißt das noch lange nicht, daß wir auch deren Größenordnung im Geiste erfaßt haben. Es gibt viele Versuche, die Größenordnung der Vorsilben zu verdeutlichen, etwa mit dem berühmten Zuckerwürfel im Bodensee. Da für uns die Wassermenge im Bodensee nicht faßbar ist, verläuft auch dieser Versuch im Sande. Im möchte die Versuche um ein Beispiel erweitern, das (so hoffe ich zumindest) leicher erfaßbar ist, da es ein Größe zum Gegenstand hat, bei der wir es gewohnt sind in mehreren Größenordnungen zu denken - die Zeit. Stellen Sie sich also vor, Sie nehmen einen Videofilm von einer Sekunde Länge auf (etwa den Flügelschlag eines Kolibris) und spielen ihn dann in Zeitlupe ab. Wenn Sie ihn so abspielen, daß eine Millisekunde (ms) im Original, einer Sekunde in Zeitlupe entspricht, so dauert die Zeitlupe fast 17 Minuten, bei einem Verhältnis vom Mikrosekunde zu Sekunde schon über 11 Tage. Entspricht eine Sekunde beim Vorführen in Zeitlupe gar einer Nanosekunde in Originalgeschwindigkeit, so müssen Sie über 31 Jahre vor dem Bildschirm sitzen, um den ganzen Film zu sehen.